دانشنامه ریاضی و کامپیوتر
سایت جامع در باب کتب و جزوات رشته های ریاضی و کامپیوتر با دانلود مستقیم.
سایت جامع در باب کتب و جزوات رشته های ریاضی و کامپیوتر با دانلود مستقیم.
The general bivariate quadratic curve can be written
|
(1)
|
Define the following quantities:
 |
(2)
|
||
|
(3)
|
|||
|
(4)
|
|||
|
(5)
|
Then the quadratics are classified into the types summarized in the following table (Beyer 1987). The real (nondegenerate) quadratics (the ellipse and its special case the circle, hyperbola, and parabola) correspond to the curves which can be created by the intersection of a plane with a (two-nappes) cone, and are therefore known as conic sections.
| curve | ||||
| coincident lines | 0 | 0 | 0 | |
| ellipse (imaginary) | ||||
| ellipse (real) | ||||
| hyperbola | ||||
| intersecting lines (imaginary) | 0 | |||
| intersecting lines (real) | 0 | |||
| parabola | 0 | |||
| parallel lines (imaginary) | 0 | 0 | ||
| parallel lines (real) | 0 | 0 |
It is always possible to eliminate the ![]() cross term by a suitable rotation of the axes. To see this, consider rotation by an arbitrary angle
cross term by a suitable rotation of the axes. To see this, consider rotation by an arbitrary angle ![]() . The rotation matrix is
. The rotation matrix is
|
(6)
|
|||
|
(7)
|
so
|
(8)
|
|||
|
(9)
|
|||
|
(10)
|
|||
|
(11)
|
|||
|
(12)
|
Plugging these into (◇) and grouping terms gives
![x^('2)(acos^2theta+csin^2theta-2bcosthetasintheta)+x^'y^'[2acosthetasintheta-2csinthetacostheta+2b(cos^2theta-sin^2theta)]+y^('2)(asin^2theta+ccos^2theta+2bcosthetasintheta)+x^'(2dcostheta-2fsintheta)+y^'(2dsintheta+2fcostheta)+g=0.](http://mathworld.wolfram.com/images/equations/QuadraticCurve/NumberedEquation2.gif) |
(13)
|
Comparing the coefficients with (◇) gives an equation of the form
|
(14)
|
where the new coefficients are
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
|||
|
(18)
|
|||
|
(19)
|
|||
|
(20)
|
The cross term ![]() can therefore be made to vanish by setting
can therefore be made to vanish by setting
|
(21)
|
|||
|
(22)
|
For ![]() to be zero, it must be true that
to be zero, it must be true that
|
(23)
|
The other components are then given with the aid of the identity
|
(24)
|
by defining
|
(25)
|
so
|
(26)
|
|||
|
(27)
|
Rotating by an angle
|
(28)
|
therefore transforms (◇) into
|
(29)
|
Completing the square,
|
(30)
|
|
(31)
|
Defining ![]() ,
, ![]() , and
, and ![]() gives
gives
|
(32)
|
If ![]() , then divide both sides by
, then divide both sides by ![]() . Defining
. Defining ![]() and
and ![]() then gives
then gives
|
(33)
|
Therefore, in an appropriate coordinate system, the general conic section can be written (dropping the primes) as
|
(34)
|
Consider an equation of the form ![]() where
where ![]() . Re-express this using
. Re-express this using ![]() and
and ![]() in the form
in the form
|
(35)
|
Therefore, rotate the coordinate system
|
(36)
|
so
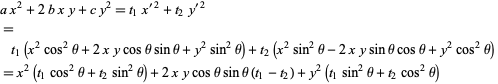 |
(37)
|
and
|
(38)
|
|||
|
(39)
|
|||
|
(40)
|
Therefore,
|
(41)
|
|||
|
(42)
|
|||
|
(43)
|
|||
|
(44)
|
|||
|
(45)
|
From (39) and (45),
|
(46)
|
the same angle as before. But
|
(47)
|
|||
|
(48)
|
|||
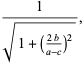 |
(49)
|
so
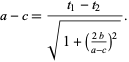 |
(50)
|
Rewriting and copying (◇),
|
(51)
|
|||
|
(52)
|
|||
|
(53)
|
Adding (52) and (53) gives
|
(54)
|
|||
|
(55)
|
Note that these roots can also be found from
|
(56)
|
|
(57)
|
|
|
(58)
|
|
|
(59)
|
|
|
(60)
|
The original problem is therefore equivalent to looking for a solution to
|
(61)
|
|
(62)
|
which gives the simultaneous equation s
|
(63)
|
Let ![]() be any point
be any point ![]() with old coordinates and
with old coordinates and ![]() be its new coordinates. Then
be its new coordinates. Then
|
(64)
|
and
|
(65)
|
|||
|
(66)
|
If ![]() and
and ![]() are both
are both ![]() , the curve is an ellipse. If
, the curve is an ellipse. If ![]() and
and ![]() are both
are both ![]() , the curve is empty. If
, the curve is empty. If ![]() and
and ![]() have opposite signs, the curve is a hyperbola. If either is 0, the curve is a parabola.
have opposite signs, the curve is a hyperbola. If either is 0, the curve is a parabola.
To find the general form of a quadratic curve in polar coordinates (as given, for example, in Moulton 1970), plug ![]() and
and ![]() into (◇) to obtain
into (◇) to obtain
|
(67)
|
|
(68)
|
Define ![]() . For
. For ![]() ,we can divide through by
,we can divide through by ![]() ,
,
|
(69)
|
Applying the quadratic formula gives
|
(70)
|
where
|
(71)
|
|||
|
(72)
|
Using the trigonometric identities
|
(73)
|
|||
|
(74)
|
it follows that
|
(75)
|
|||
|
(76)
|
|||
|
(77)
|
Defining
|
(78)
|
|||
|
(79)
|
|||
|
(80)
|
|||
|
(81)
|
|||
|
(82)
|
then gives the equation
|
(83)
|
(Moulton 1970). If ![]() , then (◇) becomes instead
, then (◇) becomes instead
|
(84)
|
Therefore, the general form of a quadratic curve in polar coordinates is given by